問題2-1
事前準備として,データを読み込みます。
dummydata_A <- read.csv("~/Dropbox/R/dummydata_A.csv")
attach(dummydata_A)
【問題1】
平均値は mean,分散は var,標準偏差は sd 関数で求めます。
mean(食費) var(食費) sd(食費)
Excel なら AVERAGE,VAR,STDEV関数で求めます。分析ツールでもいいですが,これぐらいは関数を使って求めましょう。
【問題2】
ヒストグラムは hist 関数を使って求めます。hist(食費) で作成できるのですが,これではわかりにくいので,もう少し手を入れて20001円から30000円以下の度数がわかるようにします。
par(family="HiraKakuProN-W3") #mac
par(mar=c(5,4,4,2)+0.1)
par(las=1)
par(cex=0.9)
hist(dummydata_A$食費, breaks=seq(0,230000,10000),
right = TRUE,
col = "gray",
main = "Histgram of 食費",
ylim = c(0, 2000),
xlab = "食費階級(円)(以下)", ylab = "")
axis(side=2, labels="人", at=2000,
hadj=0.6, padj=-1.5)
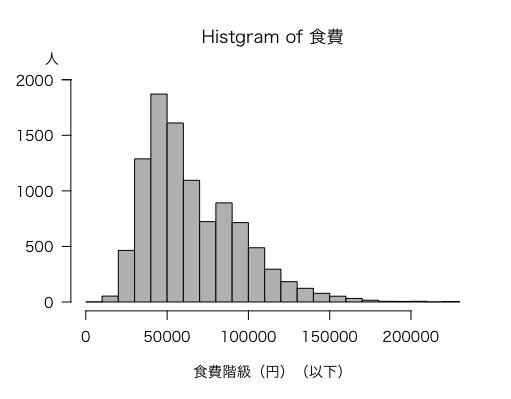
すると,次のようなヒストグラムが描けます。

なお,histのオプションについて,上限値を「以下」にするには,right = TRUE に設定します(逆に「未満」の場合は right = FALSE)
【問題3】
上に書いた【問題2】の解説でおしまい。
【問題4】
ヒストグラムの解釈の問題
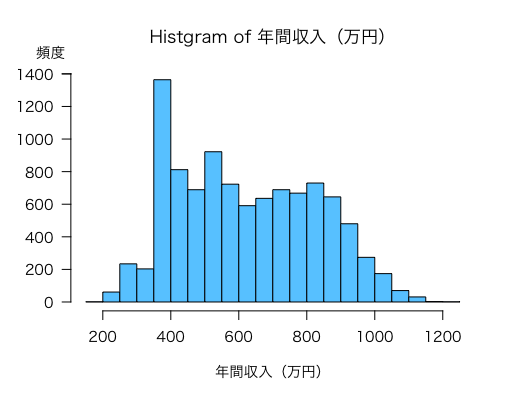
ヒストグラムから最小は200〜250万円未満の階級,最大は1100〜1150万円未満の階級であることがわかります。よって,データの分布は200〜1150万円未満になります。
最もサンプルが集中しているのは,350万円〜400万円未満の階級であることもわかります。
問題文のヒストグラムはデータが無いこともあり再現できなかったので,ここでは省略しています。
もし,dummydata_Aを使って,ヒストグラムを作るのであれば,こんな感じです。
par(family="HiraKakuProN-W3") #mac
par(mar=c(5,4,4,2)+0.1)
par(las=1)
par(cex=0.9)
income = dummydata_A$年間収入.円./10000
hist(income, breaks=seq(150,1250,50),
right = FALSE,
col = "#66ccff",
main = "Histgram of 年間収入(万円)",
xlab = "年間収入(万円)", ylab = "")
axis(side=2, labels="頻度", at=1400,
hadj=0.6, padj=-1.5)
事前に summary で最小値,最大値を求めています。また,わかりやすくするために,グラフの色を空色(#66ccff)に設定しています。また,万円単位にするために,年間収入を10000で割り,その結果を income に入れています。他,各階級の上限値を「未満」にしたいため,right = FALSE にしています。
もし,データラベルに頻度の値を入れたければ,labels = TRUE も入れておきます。
【問題5】
sd関数で標準偏差を求め,一番大きな項目が最もばらつきの大きい項目とすればいいです。