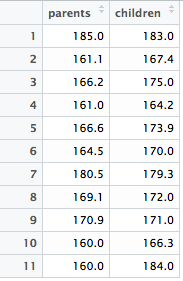
事前準備として,データを読み込みます。

hokou_W4 <- read.csv("~/Dropbox/R/hokou_data_W4.csv")
まずは散布図を描いてみます。
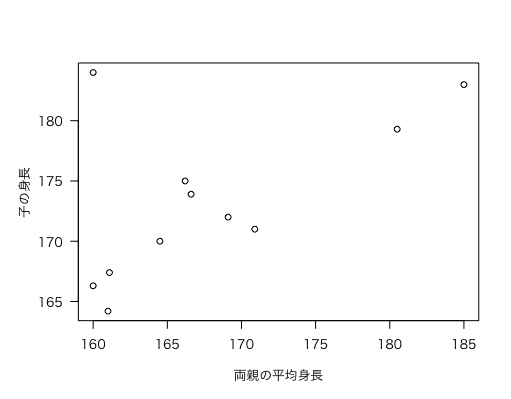
上のグラフのソース。
par(family="HiraKakuProN-W3") #mac
par(mar=c(5,5,4,2)+0.1)
par(las=1)
par(cex=0.8)
plot(hokou_data_W4$parents, hokou_data_W4$children,
xlab="両親の平均身長",
ylab="子の身長")
次に回帰分析を行ってみます。
result = lm(hokou_data_W4$children ~ hokou_data_W4$parents) sumary(result)
結果は以下の通りです。
Call:
lm(formula = children ~ parents)
Residuals:
Min 1Q Median 3Q Max
-6.049 -3.196 -1.829 1.520 14.202
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 97.5729 36.1564 2.699 0.0244 *
parents 0.4514 0.2153 2.096 0.0655 .
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 5.681 on 9 degrees of freedom
Multiple R-squared: 0.3281, Adjusted R-squared: 0.2534
F-statistic: 4.394 on 1 and 9 DF, p-value: 0.06551
モデルの決定精度である R-squared の値が 0.3281 と低くなっており,このままではモデルとして使うのは難しそうです。
散布図をよく見ると,左上に全体の傾向と異なるデータがあります(両親の平均身長 160 cm,子どもの身長 184 cm)。この外れ値を除くとどの程度改善されるのか試してみましょう。
case1 = hokou_data_W4$children < 184.0 hokou_data_W4_2 = hokou_data_W4[case1, ]
case1 という名前の変数を用意し,ここに条件(子どもの身長が184cm未満)を書き込みます。
新たに作成されたデータテーブルは次のようになります。
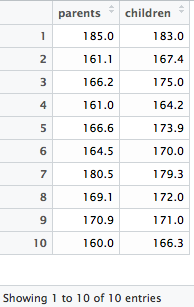
では,回帰分析をしてみます。
result2 = lm(hokou_data_W4_2$children ~ hokou_data_W4_2$parents) summary(result2)
結果は次のとおりです。
Call:
lm(formula = hokou_data_W4_2$children ~ hokou_data_W4_2$parents)
Residuals:
Min 1Q Median 3Q Max
-3.1967 -0.6216 -0.2575 0.3106 4.2616
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 63.93216 16.02921 3.988 0.004014 **
hokou_data_W4_2$parents 0.64264 0.09503 6.763 0.000143 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 2.386 on 8 degrees of freedom
Multiple R-squared: 0.8511, Adjusted R-squared: 0.8325
F-statistic: 45.73 on 1 and 8 DF, p-value: 0.0001432
決定係数が 0.8511 に向上しました。
このように外れ値は散布図を描いて目視確認するのが最も確実です。
ただし,外れ値を除外するのかの判断はデータの特性や分析目的によって異なるので注意が必要です。