問題4-1
事前準備として,データを読み込みます。
dummydata_A <- read.csv("~/Dropbox/R/dummydata_A.csv")
attach(dummydata_A)
【問題1】
回帰分析をするには,lm関数を使います。目的変数が食費,説明変数が年間収入なので次のようにします。
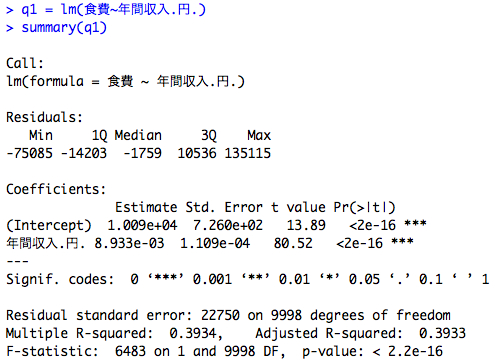
q1 = lm(食費~年間収入.円.) summary(q1)
入力例とその結果は次の図の通りです。

Multiple R-squared: 0.3934 なので,予測モデルの決定係数は 0.3934 であることがわかります。
【問題2】
Estimate のところを見ます。食費を y,年間収入.円. を x とすると,回帰方程式は y = 1.009 * 10000 + 8.933 / 1000 * x であることがわかります。x に 6000000 を代入します。
入力例とその結果は次の通りです。
> 1.009 * 10000 + 8.933 / 1000 * 6000000 [1] 63688
【問題3】
目的変数を光熱・水道費,説明変数を年間収入.円.として,回帰分析してみます。今回も lm 関数を使います。
入力例と結果は次の通りです。
> q3 = lm(光熱.水道費~年間収入.円.)
> summary(q3)
Call:
lm(formula = 光熱.水道費 ~ 年間収入.円.)
Residuals:
Min 1Q Median 3Q Max
-19366 -4890 -1162 3761 56291
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 8.063e+03 2.308e+02 34.94 <2e-16 ***
年間収入.円. 1.678e-03 3.527e-05 47.57 <2e-16 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 7233 on 9998 degrees of freedom
Multiple R-squared: 0.1846, Adjusted R-squared: 0.1845
F-statistic: 2263 on 1 and 9998 DF, p-value: < 2.2e-16
決定係数の値が 0.1846 なので,モデルの精度は低いと考えられます。
なお,散布図は次のようになります。
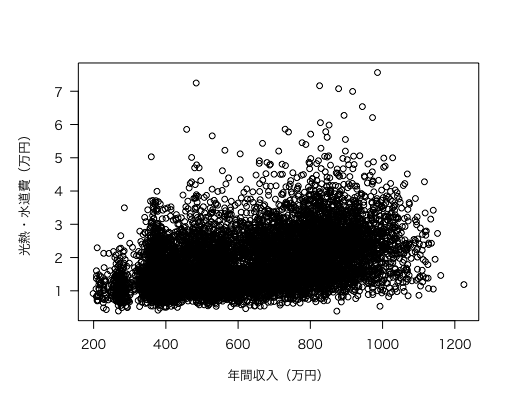
par(family="HiraKakuProN-W3") #mac
par(mar=c(5,5,4,2)+0.1)
par(las=1)
par(cex=0.8)
income = 年間収入.円./10000
heat = 光熱.水道費/10000
plot(income, heat,
xlab="年間収入(万円)",
ylab="光熱・水道費(万円)")