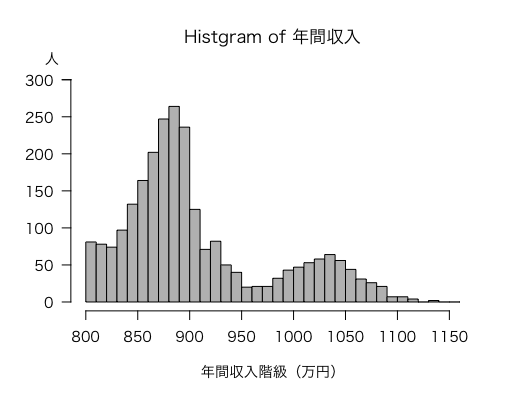
問題5-1
事前準備として,データを読み込みます。
dummydata_E <- read.csv("~/Dropbox/R/dummydata_E.csv")
attach(dummydata_E) #お好みで
【問題5-9】

ヒストグラムのソースは次の通り。
par(family="HiraKakuProN-W3") #mac
par(mar=c(5,4,4,2)+0.1)
par(las=1)
par(cex=0.9)
income = dummydata_E$年間収入.円. / 10000
h = pretty(income)
hist(income, breaks=seq(800,1160,10),
right = F,
col = "gray",
main = "Histgram of 年間収入",
ylim = c(0, max(h)),
xlab = "年間収入階級(万円)", ylab = "")
axis(side=2, labels="人", at=max(h),
hadj=0.6, padj=-1.5)
【問題5-10】
corを使って,相関係数を求めます。
> cor(年間収入.円., 教養娯楽費) [1] 0.6885426 > cor(年間収入.円., 被服及び履物費) [1] 0.1189328 > cor(年間収入.円., 食費) [1] 0.1050746 > cor(年間収入.円., 住居費) [1] -0.05196645
よって,答えは (2) になります。
【問題5-11】
工事中
【問題5-12】
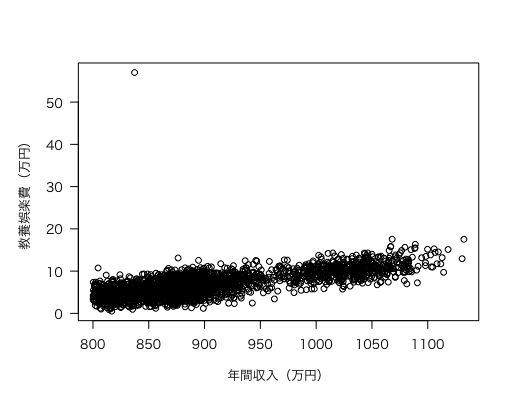
散布図のソースは次の通り。
par(family="HiraKakuProN-W3") #mac
par(mar=c(5,5,4,2)+0.1)
par(las=1)
par(cex=0.8)
income = dummydata_E$年間収入.円./10000
leisure = dummydata_E$教養娯楽費/10000
plot(income, leisure,
xlab="年間収入(万円)",
ylab="教養娯楽費(万円)")
【問題5-13】
> lm(dummydata_E$教養娯楽費~dummydata_E$年間収入.円.) Call: lm(formula = dummydata_E$教養娯楽費 ~ dummydata_E$年間収入.円.) Coefficients: (Intercept) 年間収入.円. -1.773e+05 2.724e-02
よって,答えは,(4) の y = 0.0272x - 177294 が正解。
【問題5-14】
まずは散布図を見ながら,外れ値を外す作業をします。具体的には教養娯楽費から500000円のデータを抜き,抜いたデータを dummydata_E2 とします。
> case1 = dummydata_E$教養娯楽費<500000 > dummydata_E2 = dummydata_E[case1,]
dummydata_E2 の表を元に回帰分析をします。
> lm(dummydata_E2$教養娯楽費~dummydata_E2$年間収入.円.)
Call:
lm(formula = dummydata_E2$教養娯楽費 ~ dummydata_E2$年間収入.円.)
Coefficients:
(Intercept) dummydata_E2$年間収入.円.
-1.800e+05 2.752e-02
よって,答えは,(2) の y = 0.0275x - 180042 になります。
【問題5-15】
問題5-14で求めた式の x に 10000000 を代入します。
> 0.0275*10000000-180042 [1] 94958
よって,答えは,(1) の 94,958円 になります。