石田修二ホームページ > 統計 > (サイト内検索)
英語では representative value といいます。
次の2つのグループを比べてみよう。
2つのグループを比べるときは,それぞれのグループの中心で比べるといい。手計算と mean 関数を使ってみましょう。
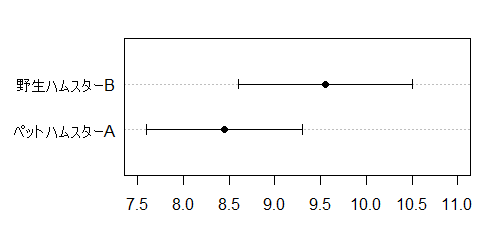
ペットハムスターAは
> (7.6+9.3)/2 [1] 8.45
mean関数を使ってみます。
> mean(c(7.6, 9.3)) [1] 8.45
野生ハムスターBは
> (8.6 + 10.5) / 2 [1] 9.55
関数を使ってみます。
> mean(c(8.6, 10.5)) [1] 9.55
したがって,8.45 < 9.55 なので,ペットハムスターより野生ハムスターの方が大きいようです。
グラフも書いてみましょう。

グラフのソース
par(mar=c(3, 6.5, 2, 1)) #下,右,上,左の余白
A = c(7.6, 9.3)
B = c(8.6, 10.5)
平均A = mean(A)
平均B = mean(B)
W = append(A, B) #ベクトルAとBを結合
dotchart(c(平均A, 平均B), pch=16,
xlim=range(c(min(W), max(W))))
arrows(A[1], 1, A[2], 1, length=0.05, angle=90, code=3)
arrows(B[1], 2, B[2], 2, length=0.05, angle=90, code=3)
mtext(c("ペットハムスターA","野生ハムスターB"), side=2, at=1:2, line=0.5, las=1)
次の2つのグループを比べてみましょう。
それぞれのグループの中心を求めればいいので,
> A = c(7.6, 8.2, 9.6); B = c(8.6, 9.8, 11.4) > mean(A); mean(B) [1] 8.466667 [1] 9.933333
したがって,8.47 < 9.93 なので,ペットハムスターより野生ハムスターの方が大きいということになります。
グラフも書いてみましょう。
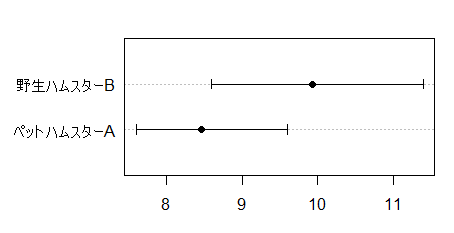
グラフのソース
par(mar=c(3, 6.5, 2, 1)) #下,右,上,左の余白
A = c(7.6, 8.2, 9.6)
B = c(8.6, 9.8, 11.4)
平均A = mean(A)
平均B = mean(B)
W = append(A, B) #ベクトルAとBを結合
dotchart(c(平均A, 平均B), pch=16,
xlim=range(c(min(W), max(W))))
arrows(A[1], 1, A[3], 1, length=0.05, angle=90, code=3)
arrows(B[1], 2, B[3], 2, length=0.05, angle=90, code=3)
mtext(c("ペットハムスターA","野生ハムスターB"), side=2, at=1:2, line=0.5, las=1)
次のデータの中央値を求めてみましょう。
ペットハムスターの体重を大きさの順に並び替えます。
> A = c(48, 57, 58, 44, 56, 36, 60, 61) > sortA = A[order(A)]
すると,36 44 48 56 57 58 60 61 の順に並びます。
> sortA[4] [1] 56 > sortA[5] [1] 57 > (sortA[4] + sortA[5]) / 2 [1] 56.5
野生ハムスターの体重も同様に並び替えます。
(工事中)
次のデータは,株価の収益率です。
このとき,1年間の平均収益率は?
(20-30+10)/3=0 というのは間違いです。これは収益率の平均であり,平均収益率ではありません。
例えば,株価を1000円として考えてみましょう。
1000円が924円に変化したのだから,先程の 0 というのは間違いということがわかります。
> x = {(1+0.2)*(1-0.3)*(1+0.1)}^(1/3)
> x
[1] 0.9739963
> x - 1
[1] -0.02600366
平均収益率は -2.6% です。
リンクはご自由にどうぞ。
Last modified: 2016-11-12 14:23:08