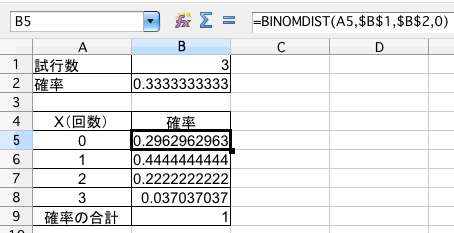
サイコロを3回投げたとき、2以下の目が出る回数を X とします。確率変数 X の分布を求めて下さい。(今野紀雄『マンガでわかる統計入門』ソフトバンククリエイティブ, 2009年, pp.130-pp.131)
Xのとりうる値は 0, 1, 2, 3です。
次に、2以下の目が出る確率を求めます。2以下の目が「1」「2」に2通りなので、2以下の目が出る確率は 1/3(←2/6を通分)になります。
X は二項分布 $\displaystyle B(3,\frac{1}{3})$ に従うので、次のようになります。

(補足)セル【B2】には =1/3(または =2/6)、セル【B5】には =BINOMDIST(A5,$B$1,$B$2,0)(または =BINOMDIST(A5,3,1/3,0))が入っています。
4枚の硬貨を同時に投げる試行を4回繰り返す時、2枚が表で2枚が裏となる回数 X の確率分布を求めよ。
X のとりうる値は 0, 1, 2, 3, 4 で、4枚の硬貨を投げて2枚とも表が出る確率は、
$\displaystyle _4 \mathrm{C} _2 (\frac{1}{2})^{2} (\frac{1}{2})^{2} = \frac{3}{8} = 0.375$
(表計算ソフトでは)=COMBIN(4,2)*0.5^2*0.5^2
よって、Xの確率分布は次のようになる。

(補足)丁寧に手書きで書けば次のようになります。
X のとりうる値は 0, 1, 2, 3, 4 で、4枚の硬貨を投げて2枚とも表が出る確率は、
$\displaystyle _4 \mathrm{C} _2 (\frac{1}{2})^{2} (\frac{1}{2})^{2} = \frac{3}{8}$
よって、X = kとなる確率 P(X = k)は
$\displaystyle _4 \mathrm{C} _k (\frac{3}{8})^{k} (\frac{5}{8})^{4-k}$
よって、Xは二項分布 $\displaystyle B(4,\frac{3}{8})$ に従う。
X = 0 の確率は $\displaystyle _4 \mathrm{C} _0 (\frac{3}{8})^{0} (\frac{5}{8})^{4} = \frac{625}{4096}$
X = 1 の確率は $\displaystyle _4 \mathrm{C} _1 (\frac{3}{8})^{1} (\frac{5}{8})^{3} = \frac{375}{1024}$
X = 2 の確率は $\displaystyle _4 \mathrm{C} _2 (\frac{3}{8})^{2} (\frac{5}{8})^{2} = \frac{675}{2048}$
X = 3 の確率は $\displaystyle _4 \mathrm{C} _3 (\frac{3}{8})^{3} (\frac{5}{8})^{1} = \frac{135}{1024}$
X = 4 の確率は $\displaystyle _4 \mathrm{C} _4 (\frac{3}{8})^{4} (\frac{5}{8})^{0} = \frac{81}{4096}$
したがって、X の確率分布は次のようになる。
| X | 0 | 1 | 2 | 3 | 4 |
| P | 625/4096 | 375/1024 | 675/2048 | 135/1024 | 81/4096 |
1つのサイコロを10回振るとき、1の目が出る回数を表す確率変数を X とする。
(1)X = k (0 ≦ k ≦ 10) となる確率 P (X = k) を求めなさい。
(2)X の期待値を求めなさい。
(3)X の標準偏差を求めなさい
(1)独立試行の定理により
$\displaystyle P(X=k)= _{10}\mathrm{C} _k (\frac{1}{6})^{k} (\frac{1}{6})^{10-k}$ (k は 0 ≦ k ≦ 10 を満たす整数)
(2)(1)から、Xは二項分布 $\displaystyle B(10,\frac{1}{6})$ に従う。
よって、求める期待値 E(X) は
$\displaystyle E(X)=10 \times \frac{1}{6} = \frac{5}{3}$
(3)工事中
どの目の出る確率も等しい1個のサイコロを繰り返して18回振るとき、1の目の出る回数 X の期待値と標準偏差を求めなさい。(皆川多喜造『確率・統計』数研出版, p.138改)
(工事中)
50歳の夫と48歳の妻が20年後まで生存する確率は、夫が 0.2、妻が 0.25 である。現在、夫が50歳、妻が48歳である10組の夫婦のうち、20年後に夫婦の少なくとも一方が生存している組の数を X とする。X が二項分布にしたがう確率変数であるとして、X の平均値、標準偏差を求めよ。(皆川多喜造『確率・統計』数研出版, p.148)

20年後に夫婦の少なくとも一方が生存する確率は、余事象を考えて、その確率を p とすると、
$p=1-(1-0.2)(1-0.25)=0.4$
平均値 m については $np=10 \times 0.4 =4$で求めても構わない。
標準偏差 σ については $\displaystyle \sqrt{npq} = \sqrt{10 \times 0.4 \times 0.6} = \sqrt{2.4} \fallingdotseq 1.55$ で求めてもOK。
リンクはご自由にどうぞ。