
1個のサイコロを5回続けて投げる。このとき、1の目が1回出る確率はいくらか。
1の目が出るという事象を○ 1以外の目が出るという事象を × で表すと、
P (○) = 1/6 P (×) = 5/6
になります。
また、5回投げて1の目が1回出るのは次の5通りです。
この場合は、5回の中から ○ を1つ選ぶ方法なので、$_5 \mathrm{C} _1 = 5$(通り)と計算できます。
さらに、これらが起こる確率はいずれも、
P (○ × × × ×) = P(× ○ × × ×) = P(× × ○ × ×) = P(× × × ○ ×) = P (× × × × ○)
= $\displaystyle (\frac{1}{6})^{1} (\frac{5}{6})^{4}$
となるので、求める確率はその和となり、
$\displaystyle _5 \mathrm{C} _1 (\frac{1}{6})^{1} (\frac{5}{6})^{4} = 0.4019$ … Ans.
(上の理屈を理解した上で、簡単に示します)

上の例ではセルの数式を次のように設定しています。
=1/6=BINOMDIST(A7,5,B3,0) (単に求めるだけなら、=BINOMDIST(1,5,1/6,0) でも構いません)[ツール]-[p値ファインダ]とクリックして、「p値計算機」ダイアログボックスに次のように入力します。
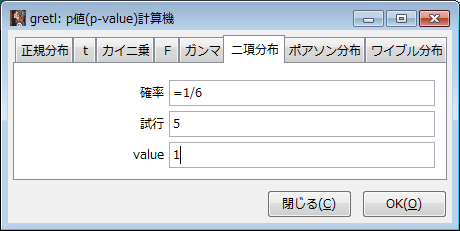
すると、以下のように結果が表示されます。答えは0.401878であることがわかります。
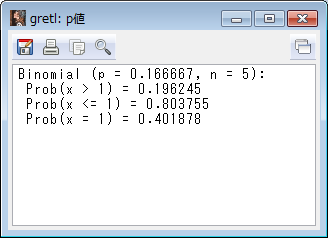
手計算、表計算ソフト、gretlでの結果を見て、0.402 ぐらいということがわかります。
4枚の硬貨を同時に投げる試行を4回繰り返す時、2枚が表で2枚が裏となる回数 X の確率分布を求めよ。
X のとりうる値は 0, 1, 2, 3, 4 で、4枚の硬貨を投げて2枚とも表が出る確率は、
$\displaystyle _4 \mathrm{C} _2 (\frac{1}{2})^{2} (\frac{1}{2})^{2} = \frac{3}{8} = 0.375$
(表計算ソフトでは)=COMBIN(4,2)*0.5^2*0.5^2
よって、Xの確率分布は次のようになる。

(補足)丁寧に手書きで書けば次のようになります。
X のとりうる値は 0, 1, 2, 3, 4 で、4枚の硬貨を投げて2枚とも表が出る確率は、
$\displaystyle _4 \mathrm{C} _2 (\frac{1}{2})^{2} (\frac{1}{2})^{2} = \frac{3}{8}$
よって、X = kとなる確率 P(X = k)は
$\displaystyle _4 \mathrm{C} _k (\frac{3}{8})^{k} (\frac{5}{8})^{4-k}$
よって、Xは二項分布 $\displaystyle B(4,\frac{3}{8})$ に従う。
X = 0 の確率は $\displaystyle _4 \mathrm{C} _0 (\frac{3}{8})^{0} (\frac{5}{8})^{4} = \frac{625}{4096}$
X = 1 の確率は $\displaystyle _4 \mathrm{C} _1 (\frac{3}{8})^{1} (\frac{5}{8})^{3} = \frac{375}{1024}$
X = 2 の確率は $\displaystyle _4 \mathrm{C} _2 (\frac{3}{8})^{2} (\frac{5}{8})^{2} = \frac{675}{2048}$
X = 3 の確率は $\displaystyle _4 \mathrm{C} _3 (\frac{3}{8})^{3} (\frac{5}{8})^{1} = \frac{135}{1024}$
X = 4 の確率は $\displaystyle _4 \mathrm{C} _4 (\frac{3}{8})^{4} (\frac{5}{8})^{0} = \frac{81}{4096}$
したがって、X の確率分布は次のようになる。
| X | 0 | 1 | 2 | 3 | 4 |
| P | 625/4096 | 375/1024 | 675/2048 | 135/1024 | 81/4096 |
1つのサイコロを10回振るとき、1の目が出る回数を表す確率変数を X とする。
(1)X = k (0 ≦ k ≦ 10) となる確率 P (X = k) を求めなさい。
(2)X の期待値を求めなさい。
(3)X の標準偏差を求めなさい
(1)独立試行の定理により
$\displaystyle P(X=k)= _{10}\mathrm{C} _k (\frac{1}{6})^{k} (\frac{1}{6})^{10-k}$ (k は 0 ≦ k ≦ 10 を満たす整数)
(2)(1)から、Xは二項分布 $\displaystyle B(10,\frac{1}{6})$ に従う。
よって、求める期待値 E(X) は
$\displaystyle E(X)=10 \times \frac{1}{6} = \frac{5}{3}$
(3)工事中
どの目の出る確率も等しい1個のサイコロを繰り返して18回振るとき、1の目の出る回数 X の期待値と標準偏差を求めなさい。(皆川多喜造『確率・統計』数研出版, p.138改)
(工事中)
1の目が出る確率が p = 0.15 であるサイコロを6回ふって少なくとも3回1の目が出る確率を求めよ。(福原文雄『社会科学系のための統計学概論 改訂版』培風館, 1990年, p.62)
1の目の出る回数を X とすると求める確率は p(X≧3) である。よって、
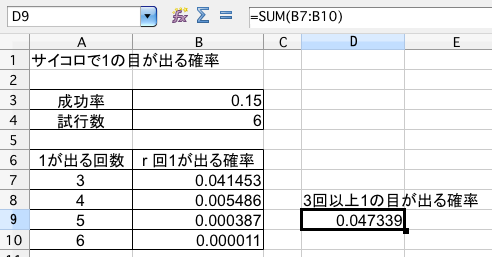
答えは、0.047339
打率3割2分の打者が20回打席に立って少なくとも8本ヒットを打つ確率を二項分布によって求めよ。(福原文雄『社会科学系のための統計学概論 改訂版』培風館, 1990年, p.77)
ヒットの本数を X とすると求める確率は p (X ≧ 8) である。よって、
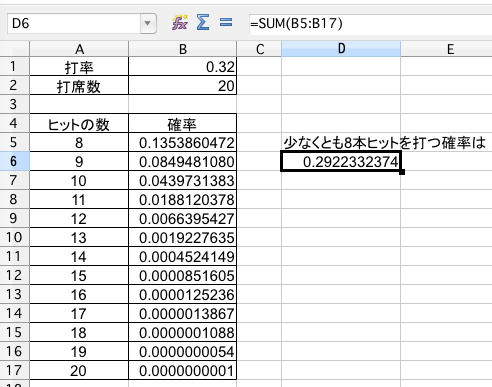
答えは、0.292233
4人の子どもを持つ世帯2,000を調べた時、(1)男の子1人、(2)男の子2人、(3)男の子3人、(4)男の子4人、の世帯はほぼいくらか。(藤沢偉作『統計の初歩』現代数学社, 1993年, p.48)
最終的の求めなければならないのは世帯数であることに注意。確率ではない。
表計算ソフトでの計算は次の通り。

セルの式については、例えば、セル【B4】には =BINOMDIST(A4,4,1/2,0)が、世帯数のセル【C4】には、=$B$1*B4 が入っている。
整理すると答えは、次のようになる。
ある列車のグリーン車は60席あり、予約しても乗車しない空席の確率は 0.05(5%)である。今、60席すべてが予約されているとき、空席が 1 以下である確率を求めなさい。(出典:小寺平治『新統計入門』裳華房, 1996年, p.63)
リンクはご自由にどうぞ。