ある変数 X の値を調べようとする時、調べるたびに値が変わってしまう変数を確率変数 (random variable) といいます。
サイコロ投げを例に説明しましょう。サイコロを投げると、1から6までのいずれか1つの目が必ず出ます。しかし、インチキでもしない限り、投げる前はどの目が出るかわかりません。このようにサイコロを投げたとき出る目の数のことを
「コインを1回投げた時のコインの表裏」「サイコロを1回投げた時の目」は確率変数としてイメージしやすいですが、統計学では「駅の窓口に並んでいる列の次の人が男性か女性か」「自動車事故での死傷者数」などの社会的事象まで、一見確率的とは思えない広範な対象についても確率変数であることを仮定していることに注意して下さい。
次のうち,確率変数(いろいろな値を確率的にとる変数)とは最も考えにくいものを選びなさい。(日本統計学会編『統計学II』p146)
(答え)1. X + 3 = 5 から求めた X = 2
(解説)
次の4つの変数のうち、確率変数と考えられない変数はどれか。一つ選びなさい。(gacco「統計学II」問題3)
(答え)3. 富士山の高さ
確率変数と一緒にもう一つ大事な概念である確率分布については、次の問題を読んで理解しましょう。定番の説明です。
(例)2枚のコインを投げるとき、表が出た枚数 X の確率分布を求めてみましょう。
同様に確からしい事象に分けてみます。
(表、表)、(表、裏)、(裏、表)、(裏、裏)
X の値は、これに、それぞれ 2, 1, 1, 0 が対応します。X の値 0, 1, 2 で場合を分けると X の確率分布は、下の表のようになります。
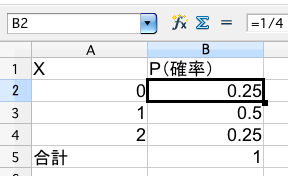
| X | 0 | 1 | 2 | 計 |
| P | 1/4 | 1/2 | 1/4 | 1 |
表計算ソフトで書けば下のような感じです。上の表とは縦横が異なっていますが、そんなことはどうでも構いません。

上の表のような対応関係をXの確率分布、表そのものは確率分布表といいます。
確率分布は大きく分けると離散分布と連続分布があり、その下に様々な分布があります。以下にその一例を示しておきます。
詳しい話はまた別のページ(工事中)で。
2つのサイコロを振って、出る目の和をXとするとき、確率変数Xの確率分布表を作成せよ。(九州歯科大)
(考え方)X のとる値は、2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12 のいずれかで、その場合の確率を求めます。
(解答)
X=2の場合 (1, 1) 1通り
よって、P = 1/36
3の場合 (1, 2) (2, 1) 2通り
よって、P = 2/36
4の場合 (1, 3) (2, 2) (3, 1) 3通り
よって、P = 3/36
5の場合 (1, 4) (2, 3) (3, 2) (4, 1) 4通り
よって、P = 4/36
6の場合 (1, 5) (2, 4) (3, 3) (4, 2) (5, 1) 5通り
よって、P = 5/36
7の場合 (1, 6) (2, 5) (3, 4) (4, 3) (5, 2) (6, 1) 6通り
よって、P = 6/36
8の場合 (2, 6) (3, 5) (4, 4) (5, 3) (6, 2) 5通り
よって、P = 5/36
9の場合 (3, 6) (4, 5) (5, 4) (6, 3) 4通り
よって、P = 4/36
10の場合 (4, 6) (5, 5) (6, 4) 3通り
よって、P = 3/36
11の場合 (5, 6) (6, 5) 2通り
よって、P = 2/36
12の場合 (6, 6) 1通り
よって、P = 1/36
以上より、求める確率分布は次のようになります。
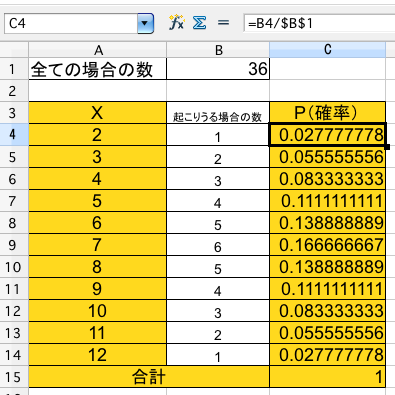
| X | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| P | 1/36 | 2/36 | 3/36 | 4/36 | 5/36 | 6/36 | 5/36 | 4/36 | 3/36 | 2/36 | 1/36 |
表計算ソフトで書けばこんな感じです。セルに色が塗られているところが大事なところです。
つぼの中に4個の白球と3個の白球が入っている。このつぼの中から、同時に3球を取り出すとき、それに含まれる白球の個数 X の確率分布を求めなさい。
Xのとる値は 0, 1, 2, 3のいずれか。
(以下工事中)
的で矢を射るのに、Aさんは5本中4本、Bさんは4本中3本、Cさんは2本中1本の割合で当てるという。3人が同時に射る時、的に当てた人の数をX人とすると、Xは確率変数である。Xの確率分布を求めよ。(『確率統計』p.120より)
Xのとりうる値は、0, 1, 2, 3 のいずれかです。X = r となる確率を prとします。
(以下工事中)
リンクはご自由にどうぞ。