期待値で判断すれば、同じことなのに、質問の仕方で異なる判断を下してしまうことはよくあります。印南一路『すぐれた意思決定』(中公新書, p.115)にこんな例があります。
(問1)あなたはどちらを選びますか。
続けて、この問題もどちらか選んで下さい。
(問2)あなたは、200ドルの非常に美しいが割れやすいガラス細工を持っています。確率25%で割れるとして、保険料として50ドル支払いますか。
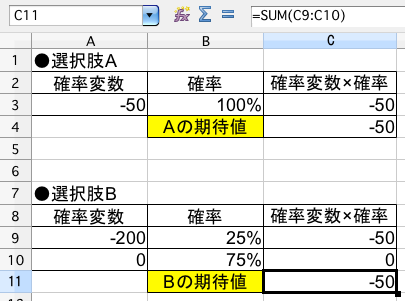
まず(問1)について、選択肢(A) (B) の期待値を計算してみます。

つまりどちらも 期待値は -50ドル であり、どちらを選んでも同じことということがわかります。
次に(問2)について、、選択肢(A) (B) の期待値を計算してみます。
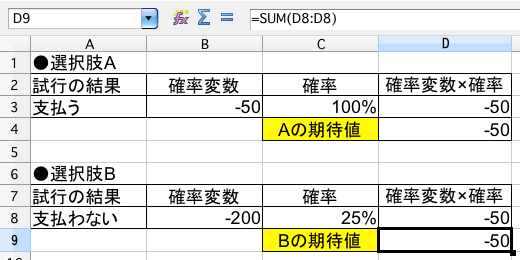
こちらも(問1)同様、期待値は同じ -50ドル です。
2つの計算を見ると、(問1)(問2)ともに選択肢A、選択肢Bが同じことを言っていることがわかります(Aの確率は100%、Bの確率は25%)。したがって、(問1)で選択肢Aを選んだ人は(問2)でも選択肢Aを選ぶのが合理的な判断ということになります。
しかし、印南先生の本によると、(問1)については、約80%の人が選択肢Bを選ぶ一方で、(問2)については回答者の65%が保険料を支払う、つまり50ドルの確実な損失を選んだそうです。
なぜ、このような結果になったのか、印南先生は、次のように解釈しています。
どんな事象においても、全く同じ選択が保険という形で表現されると、ほとんどの人はリスクを求めるよりも「リスクを避ける」ようになる。
リンクはご自由にどうぞ。