正規分布を利用して確率を求めてみましょう。
Excelでの操作方法ならびにデータの解釈はこちらにまとめました。
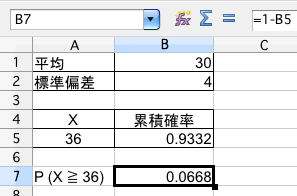
確率分布 X が正規分布 $N (30, 4^{2})$ にしたがうとき、次の確率を求めなさい。
(1の解答)答えは 0.0668
表計算ソフトでの計算は次の通り。

セル B5 には =NORMDIST(A5,B1,B2,1) が入っています。答えはセルB7に表示されている 0.0668 になります。なお、小数点の桁表示を増やせば、もっと細かい数字が出ます。
R で求める場合は、pnorm(36, mean = 30, sd = 4, lower.tail = FALSE) と入力します。するとちゃんと 表計算ソフトと同じように約 0.0668 になります。
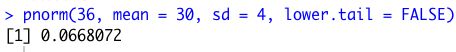
(2の解答)答えは 0.1359
R で求める場合は、次のように入力します(今回はオプション mean, sd, lower.tail = TRUE ともに省略しました)。
pnorm(26, 30, 4) - pnorm(22, 30, 4)
![]()
ちゃんと 0.1359 と答えが出ています。
ある時間帯にAB間を運行するバスの平均所要時間は 35分、標準偏差は7分である。A でこのバスに乗った乗客が B に着くのに50分以上かかる確率を求めて下さい。(福原文雄『社会科学系のための統計学概論 改訂版』培風館, 1990年, p.78)
(解答)0.0161
表計算ソフトでの計算は次の通りです。
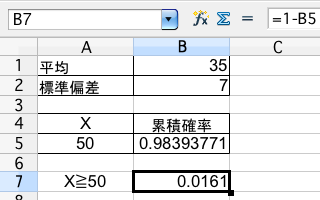
セル B5 には =NORMDIST(A5,B1,B2,1) が入っています。上側確率を求めるので、最後、セル B7 には =1-B5 が入っています。
ある部品の直径は正規分布と考えられる。直径の許容限界が 0.496 から 0.508 インチであるとき、200個の標本の直径の平均は 0.502 インチ、標準偏差 0.005 インチであった。不良品の比率を求めなさい。((藤沢偉作『統計の初歩』現代数学社, 1993年, p.59)
(解答)0.2301(約 23%)
表計算ソフトでの計算は次の通りです。
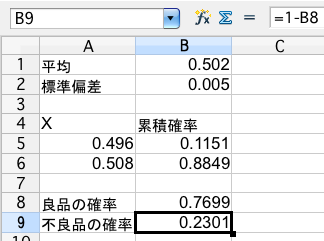
セル B5 には =NORMDIST(A5,B$1,B$2,1)、B6 には =NORMDIST(A6,B$1,B$2,1)、そしてセル B8 は良品の確率として =B6-B5 が入っています。不良品の確率は全体の確率から良品の確率を引けばよいので、セル B9 は =1-B8 となっています。
リンクはご自由にどうぞ。