Excelでの操作方法ならびにデータの解釈はこちらにまとめました。
ある高校の、3年男子500人の身長 X が、平均値 170.0cm、標準偏差 5.5cm の正規分布にしたがうものとします。このとき、
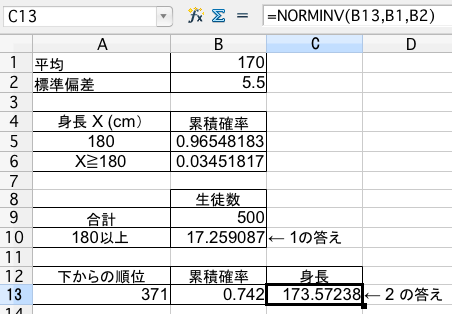
まずは答えを示します。(1)約 17 人(2)174 cm 以上になります。
表計算ソフトでの計算は次の通り。

セルの数式は次の通りです。
=NORMDIST(A4,B1,B2,1)=1-B5 全体の確率 1(100%)から B5 の確率を引き算しているだけです。=B9*B6=500-129 Excelの関数の性質を考慮して、(500人中)上位129位というのを下からの順位に変換しています。=A13/500 371人は500人の何パーセントになるか計算しています。=NORMINV(B13,B1,B2)あるクラスの語学の試験結果は、150点満点で平均94、標準偏差24の正規分布で近似することができるという。
(福原文雄『社会科学系のための統計学概論 改訂版』培風館, 1990年, p.77)
(1)0.35383
(2)139点以上の人
定員120人の入試に680人が応募しました。応募者の得点分布が、320点満点で、平均154点・標準偏差40点の正規分布とするとき、
(小寺平治『新統計入門』裳華房, 1996年, p.63)
(1)ほぼ85番
(2)約192点
ある種の犬の体重 XA (kg) が正規分布 N(10, 9) に従い、愛犬家の体重 XB (kg) が N(54, 36) に従うものとする。
(小寺平治『新統計入門』裳華房, 1996年, p.63)
(1)工事中
(2)0.72
リンクはご自由にどうぞ。