「たいすうのほうそく」と読みます。「だいすう」ではありません^^;
0または1をランダムに繰り返し発生させ全試行数のうち「1」の出現回数が果たして0.5に近いのか以下の条件で検討してみよう。
「ちょうど 0.5 が出た場合はどうするか」という疑問を持つかもしれないが、結論から言えば気にしない。というのもちょうど 0.5 が出る確率はほぼ 0 と考えてよいからである。
以下の画像はLibreOffice.org calcというソフトのものですが、Excelでもやり方は同じです。
(1)1行目に以下のような項目タイトルをつけておく

(2)まずは100回の結果を知りたいので、A列に1から100までの数字を入れておく
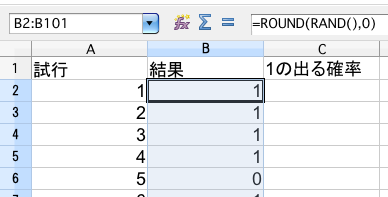
(3)1回目の結果を入れてみる。セル【B2】に =ROUND(RAND(), 0) と入力する。入力できたら100回目のセルまでコピーする

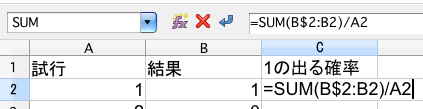
(4)【C】列に「1」の出現比率を求める。セル【C2】に =sum(B$2:B2)/A2 と入力する。入力できたら、これも100回目のセルまでコピーする

500回、1000回まで設定すると 1 の出現比率がよくわかります。
次にこれを折れ線グラフにしてみましょう。そうすると、一層わかりやすくなります。
これは偶然でしょうか。いえいえ、偶然ではありません。このようにある偶然の出来事を何度も繰り返した場合、その結果は本来の確率に近づいていきます。これを「大数の法則」といいます。大数の法則は確率論の基本的な法則です・理論的にはかたよりのないコインを無限回投げれば、表と裏の確率はちょうど 1/2 (=50%) ずつになるのです。
例えば表が9回連続して出た場合、ある人は「9回も続けて表が出たのだから、次は表は出にくいだろう」と考えるかもしれません。あるいは別の人は「次も表が出やすいだろう」と考えるかもしれません。
しかし、これらの考え方はいずれも誤りです。表と裏の確率が1/2ずつのコインであれば、過去の結果に関係なく、いつでも 1/2 の確率で表(あるいは裏)が出ます。コインやサイコロでは過去の結果は未来に影響しません。
このように、確率というものは、短期的に見る(コインを投げる回数が少ない)と、本来の確率から外れて“荒れる”ことがあります。しかし長期的に見る(コインを投げる回数が多い)と、本来の確率に近い“落ち着いた”結果が出ます。しかし、確率論の恩恵が出るまで
LibreOffice.orgで作成したファイルをここからダウンロードできます。Excelでは開くことはできません。
歪みのないサイコロを n 回(n は大きいとする)投げ、各目の出た回数を記録する。次の a.~d.の 記述のうちから、不適切なものを一つ選びなさい。(gacco「統計学II:推測統計の方法」week1 確認テスト【問題4】より)
大数の法則の観点から考えます。大数の法則は n が大きい時に相対頻度が確率に近づくことを主張しています。このことから 1 と 2 は正しいことがわかります。また偶数の目の頻度と奇数の目の頻度はともに n/2 に近いですが、これらの比をとると n が相殺されるため、これらの比が 1 に近いことも正しいです。
しかし、比が 1 に近くても、標準偏差を考えると、差の絶対値は確率的には大きくなるため、差が 0 に近いとは言えません。差の大きさをより詳しく考えるには、中心極限定理を用いる必要があります。
n が大きくなると,0から大きくなる場合もあります。nが100と100000の場合では100000の場合は偶数と奇数の頻度の差は大きくなることが予想されます。
このページの作成には次の資料を参考にしています。