
(注)組合せはこちらのページに移転しました。
$$
_n \mathrm{P} _r
$$
Excelには、PERMUT関数が用意されています。
(注)人によっては 階乗を求める FACT関数を使う人もいますが、ここでは PERMUT関数 を使います。
(例題1)1から4までの数字を書いた4枚のカードを使って、2桁の整数を作りたい。何通りできるか。
(解答と解説)表計算ソフト(LibreOffice)で求めた結果は次のとおり。Excelでも結果は同じです。

答えは 12 通りになります。
ちなみに、関数の設定画面は次の通り。n のところが Excel では「標本数」、r のところが「抜き取り数」と表示されます。
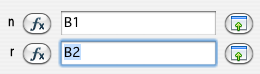
ちなみに、手で書いて求めるのであれば、次のようになります。
$ _4 \mathrm{P} _3 = 4\times 3 = 12$ Ans. 12 通り
(例題2)A, B, C, D, E, F, G, H の8人のうち、一人を議長に、もう一人を副議長に選ぶ方法は何通りあるか。
(解答と解説)表計算ソフト(LibreOffice)で求めた結果は次のとおり。

答えは 56 通りです。
ちなみに、手で書いて求めるのであれば、次のようになります。
$ _8 \mathrm{P} _2 = 8\times 7 = 56$ Ans. 56 通り
では次の問題にもチャレンジしてみて下さい。
(問題)赤・白・青・黄・緑のカードが1枚ずつある。この中から、カードを次の枚数だけとって、1列に並べる時、それぞれ、何通りの異なる並べ方があるか。
(1)2枚 (2)3枚 (3)4枚 (4)5枚
(問題)会議室に8つのいすが並んでいるとき、3人の人が席につく方法は何通りあるか。
(問題)20人の生徒から、委員長、副委員長、書記を1人ずつ選ぶ方法は何通りあるか。
(問題)次の問に答えなさい。
(1)先生1人と生徒8人が横に1列並ぶ方法は何通りあるか。
(2)(1)で先生は必ず列の端に並ぶとした場合、並び方は何通りあるか。
$$
_n \mathrm{C} _r
$$
Excelには、COMBIN関数が用意されている。
(例題)20人の生徒の中から、4人のリレー選手を決めたい。ただし、20人のうちの誰が選ばれてもよいものとする。次の場合、決め方は何通りあるか。
(1)リレーのときに走る順番を考えてきめるとき。
(2)走る順番までは考えないで選ぶとき
(考え方)
(1)走る順序を考えてきめることは、順列の数を求めることです。
(2)走る順序を考えないで選ぶことは、組み合わせの数を求めることです。
(解答)
(1)走る順番まで考えると20人の中から4人をとる順列だから
$20\times 19\times 18\times 17 = 116280$ Ans. 116280 通り
(2)走る順番を考えないで20人から4人取る組み合わせだから
$\displaystyle \frac{20\times 19\times 18\times 17}{4\times 3\times 2\times 1} = 4845$ Ans. 4845 通り
(問題)ある家の家族7人が、博覧会へ行くのに、中型、小型の2台の自動車に乗って行くことにしました。中型に4人、小型に3人乗るとして、中型と小型と分乗する分かれ方は何通りあるか。
(例題)次のような仕方は何通りあるか。
(1)男子10人から委員3人を選ぶ仕方
(2)男子10人、女子8人のうちから、男子3人、女子2人を選ぶ仕方
(解答)
(1)$\displaystyle _{10} \mathrm{C} _3 = \frac{10\times 9\times 8}{3\times 2\times 1}=120$ Ans. 120 通り
(2)男子10人から3人選ぶ仕方は $_{10} \mathrm{C} _3$ 通り、女子8人から2人を選ぶ仕方は $_8 \mathrm{C} _2$ 通り。したがって、積の法則により求める仕方の数は
$\displaystyle _{10} \mathrm{C} _3 \times _8 \mathrm{C} _2 = 120 \times 28 = \frac{10\times 9\times 8}{3\times 2\times 1} \times \frac{8\times 7}{2\times 1} = 3360$ Ans. 3360 通り