
順列や組合せの考え方と合わせながら、確率の計算をやってみましょう
ポイントは起こりうるすべての場合の数を正しく求められるかどうかです。
(例題1)男子6人、女子4人の中から、委員長・副委員長・書記を選ぶとき、3人とも男子から選ばれる確率を求めましょう。
(解答と解説)
表計算ソフトを用いた場合は次の通りです。

ノートに書く場合は次のようになります。
10人から3人をとる順列の数 $10\times 9\times 8 = 720$(通り)
男子6人から3人をとる順列の数 $6\times 5\times 4 = 120$(通り)
したがって、求める確率は $\displaystyle \frac{120}{720} = \frac{1}{6}$ … Ans.
(例題2)1から10までの番号を書いた10枚のカードの中から、同時に2枚を取り出すとき、その2枚の番号が続いた番号になっている確率を求めましょう。
(解答と解説)
表計算ソフトを用いた場合は次の通りです。
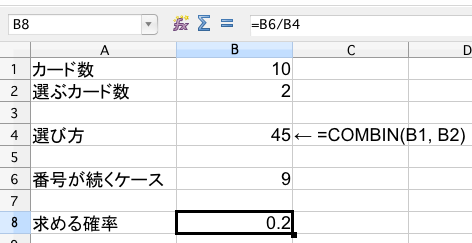
ノートに書く場合は次のようになります。
10枚のカードから2枚を取り出す場合の数は、$\displaystyle _{10} \mathrm{C} _2 = \frac{10\times 9}{2\times 1} = 45$(通り)
また、続いた番号は(1, 2), (2, 3), (3, 4), (4, 5), (5, 6), (6, 7), (7, 8), (8, 9), (9, 10) の 9 通り
したがって、求める確率は $\displaystyle \frac{9}{45} = \frac{1}{5}$ … Ans.
(例題3)男子7人、女子4人の中から、くじびきで3人の当番を決めるとき、3人とも男子または女子である確率を求めましょう。
(解答と解説)
表計算ソフトを用いた場合は次の通りです。
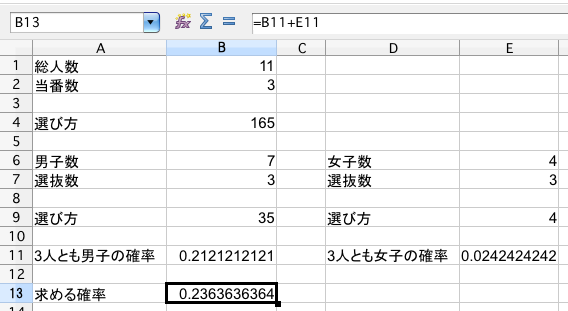
セル【B4】、【B9】、【E9】はそれぞれCOMBIN関数を使って求めています。【B4】は=COMBIN(B1,B2)、【B9】は=COMBIN(B6,B7)、【E9】は=COMBIN(E6,E7)です。
(例題4)10本のうちあたりが5本あるクジがある。このクジを、まずAさんが1本引き、続いてBさんが1本引くとき、Aさん、Bさんともに当たりである確率を求めましょう。ただし、Aさんがひいたクジは元に戻さないものとします。
(解答と解説)
表計算ソフトを用いた場合は次の通りです。
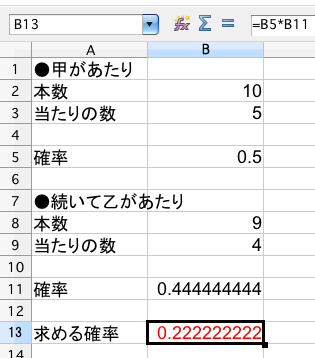
今回は関数を使っていません。
リンクはご自由にどうぞ。